Gehört zu: Statistik
Siehe auch: Streuung, Normalverteilung, Hubble
Stand: 29.12.2025
Die Fehlerbalken
Warnung / Disclaimer
Diesen Blog-Artikel schreibe ich ausschließlich zu meiner persönlichen Dokumentation; quasi als mein elektronisches persönliches Notizbuch. Wenn es Andere nützlich finden, freue ich mich, übernehme aber keinerlei Garantie für die Richtigkeit bzw. die Fehlerfreiheit meiner Notizen. Insbesondere weise ich darauf hin, dass jeder, der diese meine Notizen nutzt, das auf eigene Gefahr tut. Wenn ich Produkteigenschaften beschreibe, sind dies ausschließlich meine persönlichen Erfahrungen als Laie mit dem einen Gerät, welches ich bekommen habe.
Mittelwert
In der Physik bestimmt man Messgrößen meist in dem man eine Messung wiederholt ausführt und dann (meist) den Mittelwert aus den Einzelmessungen nimmt.
Neben dem Mittelwert einer solchen Messreihe ist aber auch noch interessant die Streuung der Messwerte und die Anzahl der Messungen. Auf grafischen Darstellungen (Diagrammen) von Messungen wird oft zusätzlich zum Mittelwert ein sog. Fehlerbalken gezeigt, der mit einem oberen und einem unteren Wert etwas über die “Genauigkeit” aussagen soll.
Streuung
Der Streubereich der Einzelwerte zeigt an, wie genau man dem Mittelwert eigentlich trauen kann. Falls die Einzelwerte normalverteilt sind, nimmt man gerne die sog. Standardabweichung (Symbol σ) als Maß für die Streuung.
Üblich als Bemessung von Fehlerbalken damit sind ±1 σ oder auch ±2 σ.
Bei einer Normalverteilung sind im Intervall ±1 σ etwa 68% und im Intervall ±2 σ etwa 95% der Werte.
Auf jeden Fall sollte man bei der Beschriftung eines Diagramms auch angeben, welche Art von Fehlerbalken dargestellt sind.
Anzahl der Messungen
Die Anzahl der Einzelmessungen einer Messreihe wird auch als Stichprobengröße (Symbol n) bezeichnet.
Bei einer sehr kleinen Stichprobengröße wird man einem errechneten Mittelwert nicht so vertrauen; bei einer größeren Anzahl Einzelmessungen wird das Vertrauen in den Mittelwert steigen. Das wird man auch durch entsprechend größere oder kleinere Fehlerbalken anzeigen wollen. Solche Fehlerbalken können verschieden berechnet werden: Standardfehler (Standard Error of the Mean SEM) oder Konfidenzintervall (CI).
Auf jeden Fall sollte man bei der Beschriftung eines Diagramms auch angeben, welche Art von Fehlerbalken dargestellt sind.
Fehlerbalken in der Praxis
In der Astronomie und der Astrophysik werden üblicherweise als Fehlerbalkentyp die ±2 σ Bemessung verwendet.
Für Konfidenzintervalle nimmt man gerne ein Konfidenzniveau von 95%.
In der Teilchenphysik (z.B. Higgs-Teilchen in CERN) gilt 5σ als sog. Goldstandard um die extrem hohe statistische Signifikanz zu beschreiben, die für eine offizielle Entdeckung erforderlich ist.
Systematische Fehler
Zusätzlich zu den oben behandelten statistischen Fehlern von Messungen, kann auch die Messmethode selbst noch systematische Fehler enthalten; diese können nur durch eine kritische Analyse des Messverfahrens selbst zu Tage gefördert werden, wobei auch Verfahren der Fehlerfortpflanzung Anwendung finden werden.
Gerne werden auch statistischer Fehlerbalken und systematischer Fehler zusammengezogen als Quadratwurzel aus der Summe der quadrierten Fehler.
Beispiel: Der Hubble-Parameter
Die Messungen des Hubble-Parameters sind ein klassisches Beispiel für Fehlerbalken-Darstellungen. Im untenstehenden Diagramm werden zwei unterschiedliche Messverfahren gegenübergestellt und wie sich die Fehlerbalken im Lauf der Jahre verändert haben.
Wenn sich die Bereiche nicht überlappen, ist der Verdacht naheliegend, dass ein signifikanter Unterschied zwischen den Messreihen besteht…
YouTube-Video: https://youtu.be/0wfPdhJWMTM?si=ExtKVnwdj9eYCisX
Abbildung 1: Hubble Tension (pCloud: fspas-05-00044-g008.jpg)
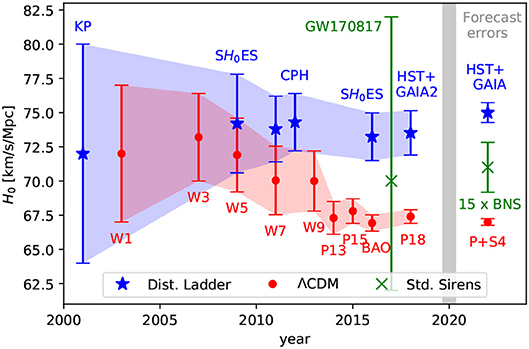
J.M.Ezquiaga, M. Zumalagarregui 2018, DOI:10.3389/fspas.2018.00044
Formeln
Die Meßreihe sei:
\( x_i (i = 1, 2 ,…,n) \\\)Dann errechnet sich der Mittelwert (Mean) der Messreihe zu:
\( \Large\bar{x} = \frac{1}{n} \sum\limits_{i=1}^{i=n} {x_i} \\\)Die Standardabweichung ist ein Maß für die Streuung der Einzelwerte der Messreihe um den ihren Mittelwert.
Diese Standardabweichung (Standard Deviation) der Messreihe berechnen wir so:
\( \Large S = \sqrt{\frac{ \sum\limits_{i=1}^{i=n} {(x_i – \bar{x}})^2 }{n-1}}\\\)Der Standard Error of the Mean (SEM) dagegen, beziffert die Genauigkeit des Mittelwerts der Messreihe in Bezug auf den “wahren” Wert; eigentlich durch mehrmalige Wiederholung der ganzen Messreihe. Dieser SEM errechnet sich ganz einfach zu:
\( SEM = \Large\frac{\sigma}{\sqrt{n}} \\\)Wobei σ die Standardabweichug der Grundgesamtheit ist, die wir aber nicht wirklich kennen. In der Praxis verwendet man als Schätzwert für σ ganz einfach die Standardabweichung der einen Messreihe, womit man erhält:
\( SEM = \Large\frac{S}{\sqrt{n}} \\\)